2.6 統計モデル、教師あり学習、関数近似

このセクションでは、教師あり学習を「関数近似」という統一的な視点で捉え直します。データの背後にある真の関数 f(x) を推定することが、すべての予測問題の本質であることを理解します。

前のセクションでは、k近傍法や線形回帰を個別のテクニックとして学びました。ここでは、これらを「同じ目標に向かう異なるアプローチ」として理解するための理論的枠組みを構築します。

なぜ「関数」を考えるのか？

あなたは今、目の前にデータの山を抱えています。入力 X と出力 Y のペアがたくさん。これを使って、まだ見ぬ新しい入力に対する出力を予測したい。

ここで立ち止まって考えてみましょう。「予測する」とは、一体何をすることなのでしょうか？

実は、予測とは関数を見つけることなのです。

入力 X を受け取り、出力 Y を返す「何か」—それが関数 f(X) です。データを観察し、この f を推定することが、教師あり学習の本質です。

しかし、現実世界は単純ではありません。同じ入力 X に対して、常に同じ出力 Y が得られるわけではないのです。天気予報を思い出してください。今日の気温や気圧（入力 X）が全く同じでも、明日の天気（出力 Y）は日によって異なります。

これはノイズ（誤差）の存在を意味します。真の関係は決定的ではなく、ランダムな要素を含んでいるのです。

真のモデル

真のモデルは以下のように表されます：

Y = f(X) + \varepsilon

ここで：

$$Y$$ は観測される出力
$$f(X)$$ は真の関数（これを見つけたい！）
$\varepsilon$ はランダムな誤差

誤差 ε について補足しましょう。「平均するとゼロになる」という性質を持ちます。プラスにもマイナスにもぶれますが、たくさん集めれば打ち消し合ってゼロに近づくのです。また、入力 X の値に関係なくランダムに発生します。

この式が意味することは深いです。私たちが観測する Y は、真の信号 f(X) とノイズ ε の和なのです。

統計モデルの意味

さて、「統計モデル」という言葉を聞いたことがあるでしょうか？難しそうに聞こえますが、考え方はシンプルです。

統計モデルとは、データがどのように生成されたかについての仮説です。

先ほどの式 $Y = f(X) + \varepsilon$ は、最もシンプルで広く使われる統計モデルの一つです。このモデルは以下を仮定しています：

加法的誤差: ノイズは出力に「足し算」される
誤差の独立性: ノイズは入力 X とは関係なく発生する
誤差の期待値ゼロ: ノイズは平均的にはゼロ（偏りがない）

なぜこのようなモデルを考えるのでしょうか？

現実世界では、入力と出力の間に完全に決定的な関係（Y = f(X) ぴったり）が成り立つことは稀です。測定誤差、観測されていない要因、本質的なランダム性など、様々な要因が結果に影響を与えます。

加法的誤差モデルは、これらすべての「予測不可能な変動」を一つの項 ε にまとめているのです。

条件付き分布

ここで「条件付き」という考え方を導入しましょう。「条件付き」とは、「ある条件のもとで」という意味です。

例えば、「入力 X が特定の値 x のとき、出力 Y はどんな値を取りやすいか？」—これが条件付き分布です。

\text{Pr}(Y|X) \text{ は } X \text{ に依存する}

この記号「Y|X」は「X が与えられたときの Y」と読みます。

加法的誤差モデルでは、「X = x のとき、Y の平均値は何か？」という問いに対して、きれいな答えが得られます：

$$E(Y|X = x) = f(x)$$

E は「期待値」（平均値）を表す記号です。つまり、「入力が x のとき、出力 Y を何度も観測すれば、その平均は f(x) になる」という意味です。

教師あり学習とは何か

統計モデルで「何を推定するか」がわかったところで、次は「どうやって推定するか」を見ていきましょう。

「教師あり学習」という言葉の由来を考えてみます。

学校を想像してください。先生（教師）が問題と正解のペアを見せてくれます。生徒は、これらの例から「問題を解くルール」を学びます。そして新しい問題が出されたとき、学んだルールを使って答えを導きます。

機械学習における「教師あり学習」も、まさにこれと同じです。

訓練データ = 問題と正解のペア $$(x_i, y_i)$$
学習アルゴリズム = ルールを学ぶ生徒
関数 $\hat{f}$ = 学んだルール
新しい入力への予測 = テスト問題を解く

学習アルゴリズムは、訓練データを通じて「例から学ぶ」のです。

どのように学ぶのか

手法によってアプローチは異なりますが、共通しているのは「予測と実際のズレをできるだけ小さくする」という目標です。

線形回帰の場合：すべての訓練データを使って、一度に最適な重みを計算する
ニューラルネットワークの場合：データを少しずつ見ながら、重みを繰り返し調整する

どちらのアプローチも、最終的には「訓練データをうまく説明できる関数」を見つけようとしています。

関数近似という視点

さて、ここで重要な視点の転換があります。

これまで「学習」という言葉を使ってきましたが、数学者や統計学者は同じ問題を「関数近似」として捉えます。

なぜこの視点が重要なのでしょうか？

「学習」という言葉は人間の認知プロセスを連想させ、時にミステリアスな響きを持ちます。しかし「関数近似」という視点を取ると、問題は純粋に数学的なものになります：

「与えられたデータ点に基づいて、真の関数 f(x) を近似する関数 $\hat{f}(x)$ を構築せよ」

この視点から見ると、すべての教師あり学習手法は「関数近似の異なる戦略」として統一的に理解できます。

線形回帰: 関数を直線（またはより一般に、入力の線形結合）で近似
k近傍法: 関数を局所的な平均で近似
多項式回帰: 関数を多項式で近似
ニューラルネットワーク: 関数を複雑な非線形変換の合成で近似

これらの手法については後のセクションで詳しく学びます。今は「様々なアプローチがある」ということを覚えておいてください。

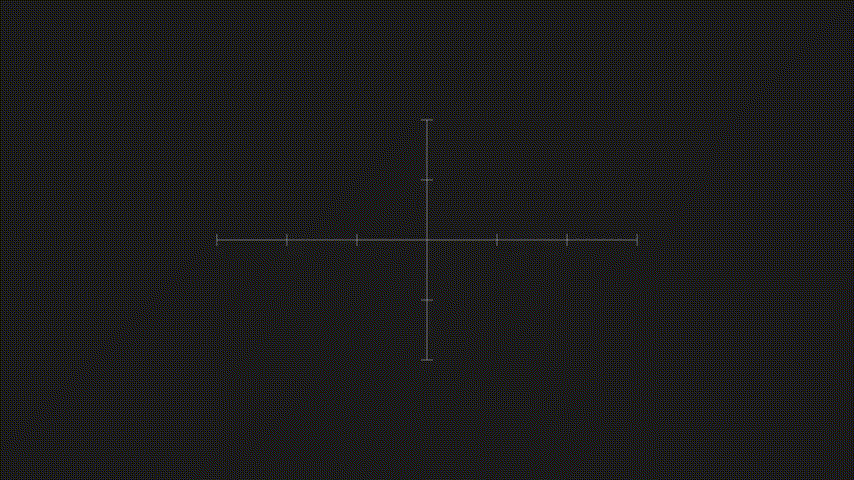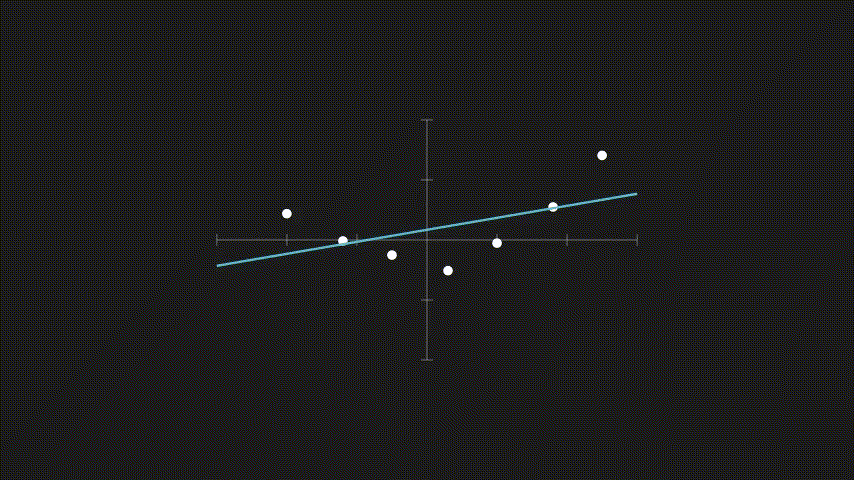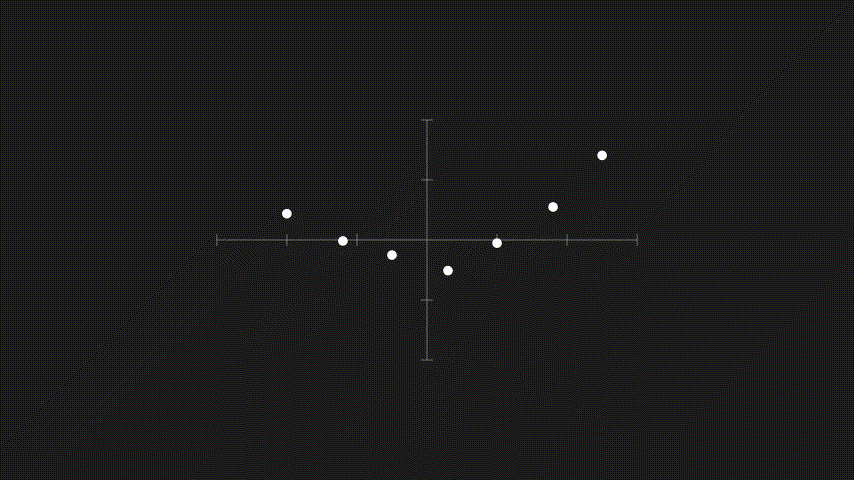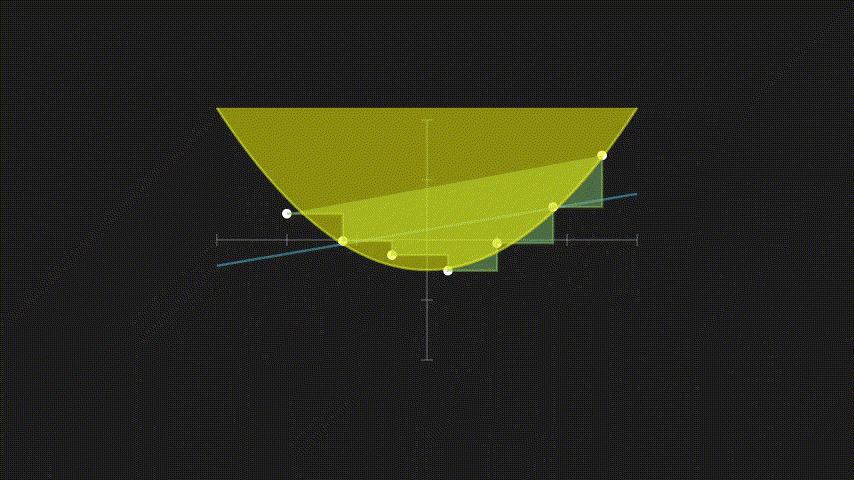
どの手法を選ぶかは、「真の関数がどのような形をしているか」についての仮定に依存します。

パラメトリックモデル

関数近似を行う最も一般的な方法は、パラメトリックモデルを使うことです。

パラメトリックモデルとは、関数の「形」をあらかじめ決めておき、データを使って「形を決めるパラメータ」を調整するアプローチです。

線形モデル

最もシンプルな例は線形モデルです：

f(x) = x_1 \beta_1 + x_2 \beta_2 + \cdots + x_p \beta_p

これは「入力の各成分に重みをかけて足し合わせる」という意味です。例えば、家の価格を予測するなら：

価格 = (面積 × 重み₁) + (築年数 × 重み₂) + (駅からの距離 × 重み₃)

ここで各重み $\beta_1, \beta_2, \beta_3, ...$ がパラメータです。これらを総称して $\theta$ （シータ）と書くこともあります。データを使って最適な重みを見つけることで、関数が決まります。

基底関数展開

より一般的には、基底関数展開と呼ばれる形式がよく使われます：

f_\theta(x) = \sum_{k=1}^{K} \theta_k h_k(x)

ここで：

$$h_k(x)$$ は基底関数（入力を変換する関数）
$\theta_k$ は各基底関数の重み（パラメータ）

基底関数の例：

多項式: $$h_k(x) = x^k$$ （x, x², x³, ...）
三角関数: $h_k(x) = \sin(kx)$ や $\cos(kx)$
シグモイド: $h_k(x) = \frac{1}{1 + e^{-x^T\beta_k}}$ （0から1の間の値を滑らかに出力する関数、ニューラルネットワークで使用）

基底関数を変えることで、驚くほど多様な関数を表現できるようになります。

最小二乗法

パラメータ $\theta$ は、通常最小二乗法で推定します。

考え方はシンプルです。「予測値と実際の値のズレを、すべてのデータ点について合計したもの」を最小化します。このズレの合計を残差平方和（RSS: Residual Sum of Squares）と呼びます：

\text{RSS}(\theta) = \sum_{i=1}^{N} (y_i - f_\theta(x_i))^2

各項 $(y_i - f_\theta(x_i))^2$ は「実際の値と予測値の差の二乗」です。二乗するのは、プラスとマイナスを打ち消さないためです。

この RSS を最小化する $\theta$ を見つけることで、データに最もフィットする関数が得られます。

なぜ最小二乗法が「正しい」のか？—最尤推定という考え方

最小二乗法は直感的にわかりやすい手法ですが、なぜこれが「正しい」のでしょうか？より深い理論的基盤があるのでしょうか？

実は、最小二乗法は最尤推定という強力な統計原理の特殊ケースなのです。

最尤推定の考え方

最尤推定の考え方は次のとおりです：

「観測されたデータが生じる確率が最も高くなるようなパラメータを選べ」

言い換えると、「今手元にあるデータが起きやすい世界を想定せよ」ということです。

加法的誤差モデルで、誤差が正規分布に従う場合を考えてみましょう。正規分布とは「ベルカーブ」とも呼ばれ、平均値の周りに値が集まりやすい分布です。身長や体重など、自然界の多くの現象がこの分布に従います。

\varepsilon \sim N(0, \sigma^2)

この記号は「誤差 ε は平均 0、ばらつき $\sigma^2$ の正規分布に従う」という意味です。

すると、出力 Y の条件付き分布は：

Y|X \sim N(f_\theta(X), \sigma^2)

つまり、Y は平均 $f_\theta(X)$ 、分散 $\sigma^2$ の正規分布に従います。

最小二乗法と最尤推定の関係

数学的な詳細は省略しますが、結論だけ述べると：

誤差が正規分布に従う場合、「データが起きやすさ」を最大化することと、「残差平方和」を最小化することは、まったく同じことになります。

つまり、最小二乗法は次のことを行っています：

\text{RSS を最小化} \Leftrightarrow \text{尤度（データの起きやすさ）を最大化}

これは重要な発見です。最小二乗法は、誤差が正規分布に従うという仮定のもとで、最も「もっともらしい」パラメータを見つけているのです。

直感的に言えば、「予測と実測のズレが小さいほど、そのモデルはデータをうまく説明している」ということになります。

まとめ—統一的な視点

このセクションで学んだことを整理しましょう。

教師あり学習は、以下の3つの視点から同じ問題を見ています：

1. 統計モデルの視点

データは $Y = f(X) + \varepsilon$ というモデルから生成される。目標は真の関数 f を推定すること。

2. 機械学習の視点

例（訓練データ）から学習し、新しい入力に対して予測を行う。学習アルゴリズムはフィードバックを通じて改善する。

3. 関数近似の視点

与えられたデータ点を説明する関数を構築する。パラメトリックモデルを使い、最小二乗法や最尤推定でパラメータを決定する。

これらは表現は異なりますが、本質的に同じことを述べています。

重要なのは、どの手法を選ぶかは「真の関数についてどのような仮定を置くか」に依存するということです。

関数が線形だと仮定すれば → 線形回帰
関数が局所的に一定だと仮定すれば → k近傍法
関数が滑らかだと仮定すれば → スプライン
関数が階層的な非線形変換だと仮定すれば → ニューラルネットワーク

仮定が正しければ、少ないデータでも良い予測ができます。仮定が間違っていれば、どんなにデータがあっても予測は外れます。

次のセクションでは、これらの仮定をどのように検証し、適切なモデルを選ぶかについて学びます。